Background: Markov Chains for Document Representations
Chris Tralie
Human languages, often referred to as ``natural languages,'' are rich and full of meaning. Compared to computer languages, they are much harder to automatically interpret and process. However, we can make some progress at representing natural languages using a few simple statistical ideas.
In this class, our focus will be on creating algorithms to capture the style of some given text from a set of examples. Then, we will be able to classify documents based on which documents satisfy which model better.
In the discussion below, we refer to documents that we use to build a statistical model as training data.
Zero-Order Statistical Modeling
We'll start by discussing how to synthesize text to match a style based on statistics. We'll then use the same concept to assign a probability of a string being in a particular style.
The simplest possible thing we could do to model text statistically is try to match the frequency of occurrence of the characters in a document. For example, if we use a collection of spongebob quotes, we find that we have the following character counts across all quotes:
Then, we can then try drawing characters according to these counts. For example, we'd be more likely to draw an 'i' than we would to draw a 'z', and we're more likely to get a space ' ' than any other character. If we draw 100 characters independently with these probabilities, we get text that looks like this:
- onc 5donps fwyce agoti'tm ne edoi a e Iueogd ei IralcrltItmo.g mimyheat tgesue nwierayekra fP he
- l rOxttsu Iogrmetucafo ewa khtois!e bttcatnht,r Cyfhr Pngkswhnwl oiet lyoatrl atumr e lenriadb Ie
- Gi dyuh b .di Po mmceooet'd'nne'n gdo dkimeo aanti is0o i 'uttj'Sstopfsasep!. mosltayaaSso?lraV l
Interestingly, the size of the "words" looks about right since we are more likely to choose a space than any other character, but they are total gibberish. This is because the process has no memory; each character is chosen completely independently from the character preceding it.
K-Prefixes
As it turns out, if we have just a very simple memory of a few characters, we can do a much better job at synthesizing sequences. Surprisingly, we can shoehorn the "memoryless" Markov chain framework from our class exercise into having a small memory if we change our notion of what a "state" is. In particular, a "state" will now be a small sequence of characters of length k instead of just a single character. This is referred to as a k-prefix.
As an example, let's consider that we had the string aaabaaacaabbcabcc. If we took all of the 2-prefixes of this string, we would have the following counts
In the Markov framework, we also have transitions that occur every time a new character is seen. On the above example, they would look like this:
Let's think about what these mean as transitions in the Markov chain. If we're at aa and we get an a, then we stay at aa. If we get a b, then we chop the a off of the left and move to ab. If we're at ca and we see a b, we chop the c off of the left and move to ab. And so on. Drawn as a state diagram, all such transitions look like this:
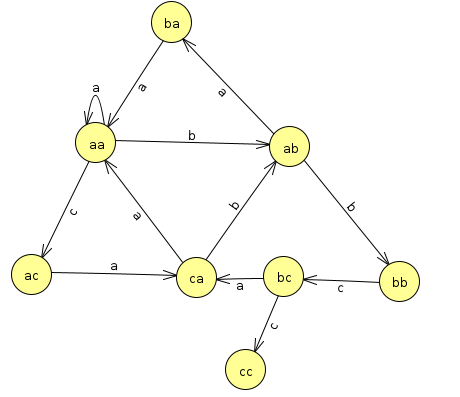
One issue with this is that it runs into a dead end at cc. This is fine if we're analyzing probabilities, but if we're doing a random walk through our model to synthesize text, we'll run into a dead end there. To make it so we can keep going, we'll loop the text around by padding the end of the string with the first k characters. In this example, this means padding the original string with the first two characters, so we create the prefixes of the string aaabaaacaabbcabccaa. That leads to the following counts for the prefixes and transitions
Notice how the count of ca->a has gone up by 1, and now there is a transition from cc->a. Now there are no dead ends in the state transitions, and we can walk through this model randomly forever to generate random strings.
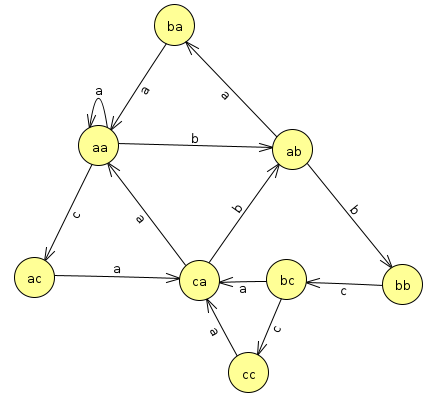
Below is a more in-depth example with some real text from the spongebob quotes text file provided with homework 3
Spongebob Example
As an example here are all of the counts of the 4-prefix 'you ' in the Spongebob text:
| New Sentence | Character Counts for 'you ' After Sentence |
| Gary, go away, can't you see I'm trying to forget you? | {"s":1} |
| Why are you mad? Because I can't see my forehead! | {"s":1, "m":1} |
| Can you take the crust off my Krabby Patty? | {"s":1, "t":1, "m":1} |
| Did you see my underwear? | {"s":2, "t":1, "m":1} |
| Well, it makes you look like a girl! | {"s":2, "t":1, "l":1, "m":1} |
| East, oh I thought you said Weest! | {"s":3, "t":1, "l":1, "m":1} |
| That's it, mister, you just lost your brain priveleges! | {"s":3, "t":1, "j":1, "l":1, "m":1} |
| I wumbo, you wumbo, he she we, wumbo, wumboing, wumbology, the study of wumbo? | {"s":3, "t":1, "w":1, "j":1, "l":1, "m":1} |
| It's not you that's got me... it's me that's got me! | {"s":3, "t":2, "w":1, "j":1, "l":1, "m":1} |
| Why don't you ask CowBob RanchPants and his friend Sir Eats-a-lot? | {"a":1, "s":3, "t":2, "w":1, "j":1, "l":1, "m":1} |
| Krusty Krab Pizza, it's the pizza for you and meeeee! | {"a":2, "s":3, "t":2, "w":1, "j":1, "l":1, "m":1} |
| If you believe in yourself, with a tiny pinch of magic all your dreams can come true! | {"a":2, "b":1, "s":3, "t":2, "w":1, "j":1, "l":1, "m":1} |
| Goodbye everyone, I'll remember you all in therapy. | {"a":3, "b":1, "s":3, "t":2, "w":1, "j":1, "l":1, "m":1} |
| Don't you have to be stupid somewhere else? | {"a":3, "b":1, "s":3, "t":2, "w":1, "h":1, "j":1, "l":1, "m":1} |
| Squidward, you can't eat all those patties at one time! | {"a":3, "b":1, "s":3, "c":1, "t":2, "w":1, "h":1, "j":1, "l":1, "m":1} |
| I'll have you know, I stubbed my toe last week, while watering my spice garden, and I only cried for 20 minutes. | {"a":3, "b":1, "s":3, "c":1, "t":2, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Squidward, you and your nose will definitely not fit in. | {"a":4, "b":1, "s":3, "c":1, "t":2, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Who you callin' pinhead? | {"a":4, "b":1, "s":3, "c":2, "t":2, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Gee Patrick, I didn't know you could speak bird. | {"a":4, "b":1, "s":3, "c":3, "t":2, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Any particular reason you took your pants off. | {"a":4, "b":1, "s":3, "c":3, "t":3, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Let me get this straight, you two ordered a giant screen television just so you could play in the box? | {"a":4, "b":1, "s":3, "c":4, "t":4, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| I'd hate you even if I didn't hate you. | {"a":4, "b":1, "s":3, "c":4, "t":4, "e":1, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| You're a man now, Spongebob, and it's time you started acting like one. | {"a":4, "b":1, "s":4, "c":4, "t":4, "e":1, "w":1, "h":1, "j":1, "k":1, "l":1, "m":1} |
| Can you give Spongebob his brain back, I had to borrow it for a week. | {"a":4, "b":1, "c":4, "e":1, "g":1, "h":1, "j":1, "k":1, "l":1, "m":1, "s":4, "t":4, "w":1} |
Synthesizing Text
Now, let's say we do the following steps, starting with the prefix 'you ':- We randomly choose one of the characters that's to follow, and we choose a 'c'
- We then slide over by one character move onto the next prefix, which is 'ou c'. We then see the character counts {"a":2, "o":2} for that prefix.
- We make another random choice at this point, and we draw the character 'a'. So then we slide onto the prefix 'u ca', and we see the counts {"l":1, "n":1} for that prefix.
- We now make a random choice and draw the character 'n'. We then slide over to the prefix ' can', and we see the counts {" ":3, "'":4}
- We now make a random choice and draw a space, so we slide over to the prefix 'can ', and we see the counts {"c":1, "h":1, "I":1}
- We now make a random choice of an h, moving us to the prefix 'an h', and so on and so forth
- you can have facial hair!Now than 24, 25.You don't need a new I stupid
- you can have to die right.You know the true!If your secrets is hot burns down
- you can have feet?Since who can't you.I'd hate you and I'm absorbing
- you can have to be alright.If I wish is nothere ther.No, Patty?
As you can see, this text is starting to make a lot more sense than choosing each character independently, even with a very short memory.
The Probability of A Sequence
In addition to synthesizing text in a model trained on k-prefixes from a particular set of documents, we can assess how likely a different document is to be in the style that we've modeled with our Markov chains. To do this, we will compute the probability of a particular sequence given a model. Markov chains have a simplifying assumption of independence that will help make this easier to compute. In particular, the next character is chosen only based on the current prefix, and none of the previous prefixes influence this decision.
Independent events are nice to work with because the probability of independent events occurring is a simple multiplication. For example, it's reasonable to assume that the type of weather in Beijing on a particular day is independent of the weather in Collegeville. So if the probability it rains in Collegeville is 0.4 and the probability it rains in Beijing is 0.6, then the joint probability of both occurring is 0.4 x 0.6 = 0.24
To compute the probability of a particular sequence of characters, we must first compute the probability that each character was drawn under our model, and then we may compute the joint probability of the entire sequence by multiplying them together. The probability of a particular character c preceded by the prefix p is given as
\[ p(c) = \frac{N(p.c) + 1}{N(p)+S} \]
where
-
N(p)is the number of times the prefix occurs in the model (which can be 0) -
N(p.c)is the number of times the charactercfollows prefixp(which can be 0, and which is automatically 0 if the prefix doesn't exist in the model) -
Sis the size of the alphabet in the model (i.e. the number of unique characters across all prefixes)
N(p.c) and N(p) are 0, and the probability is 1/S
There is a slight numerical issue with the above scheme, however. Since there are many characters in most sequences of interest, and since the probabilities of each character are small, we can run into arithmetic underflow where the multiplication of many small numbers ends up just bottoming out at zero numerically. To get around this, we can instead compute the ``log probability''. Since \[ \log(AB) = \log(A) + \log(B) \] We can compute the log of the product probabilities as the sum of the log of each probability. So simply modify the formula as \[ \log \left( p(c) \right) = \log \left( \frac{N(p.c) + 1}{N(p)+S} \right) \] and then sum all of these up for each character to get the final log probability.
Simple Example
Let's consider a fully fledge simple example. Let's suppose that we added the string aaacbaaaacabacbbcabcccbccaaac to the model and we considered all 3-prefixes, so that we have these counts in the model (considering the wrap-around)
Now let's say we wanted to compute the probability of the string aacabaa given the the model. There are three unique characters in the alphabet here: a, b, and c, so S = 3. Then, we compute the probability of each chunk aac, aca, cab, aba (all substrings of length 3 with at least one character following them)
| p | N(p) | c | N(p.c) | \[ \log \left( \frac{N(p.c) + 1}{N(p)+S} \right) \] |
| aac | 3 | a | 2 | = log(2 + 1) / (3 + 3) = -0.6931 |
| aca | 2 | b | 1 | = log(1 + 1) / (2 + 3) = -0.9163 |
| cab | 2 | a | 1 | = log(1 + 1) / (2 + 3) = -0.9163 |
| aba | 1 | a | 0 | = log(0 + 1) / (1 + 3) = -1.386 |
Summing all of these up, we get -3.91