Softmax (Multi-Class Classification)

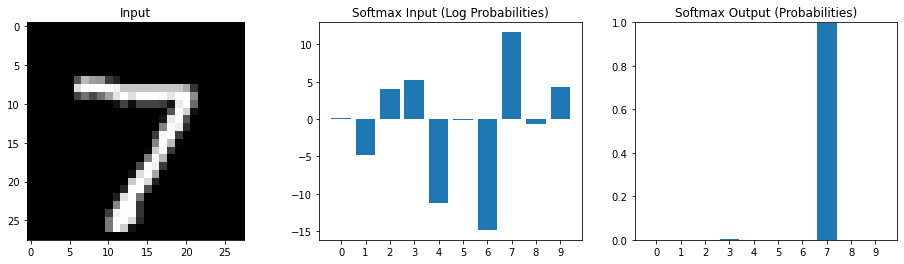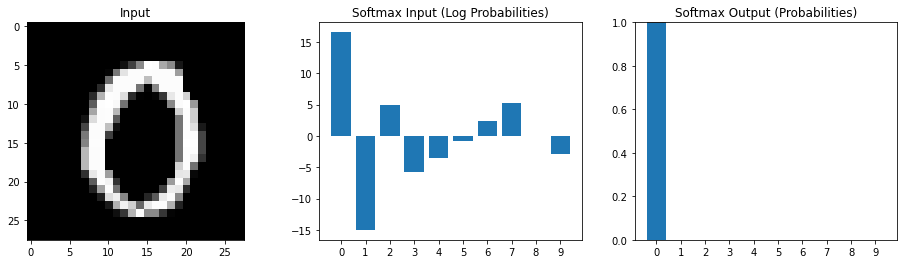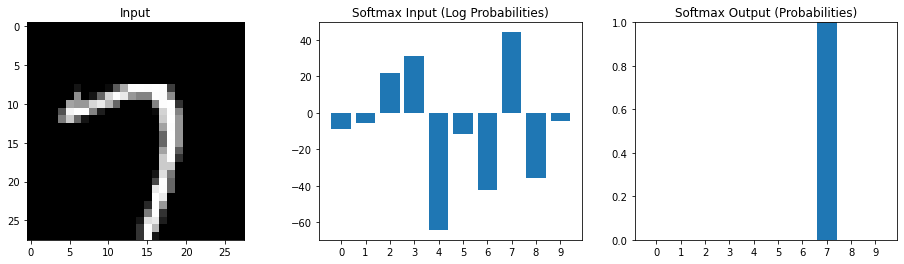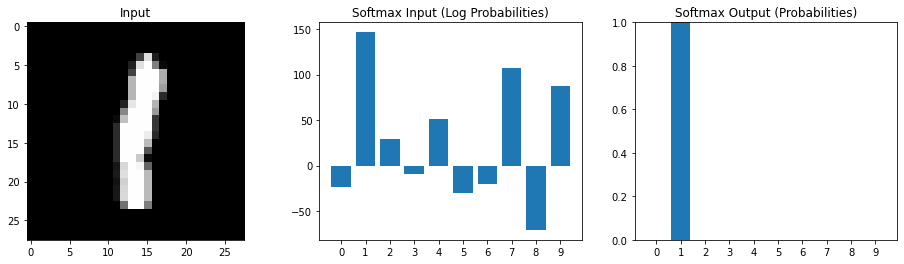
Multiple possible outputs

	Activation Function	Loss Function
Logistic Regression (Binary Classification)	Logistic Function: $\frac{1}{1+e^{-u}}$	Logistic loss
Multi-Class Logistic Regression (Learn one of many options)	Vector u as input $\sigma_{sm}(\vec{u})_i = \frac{e^{u_i}}{\sum_{j = 1}^{L} e^{u_j}}$	Binary Cross-Entropy (BCE)

Softmax emphasizes relatively larger values

• Each element of the softmax is nonnegative
• The sum of of all of the elements is 1

Interpret the input the softmax as log probabilities Output of softmax as estimated probabilities

For multi-class classification, we're going to have a multidimensional "ground truth" $y$ that we aspire to. So I'll define something called the "one-hot vector" $\vec{y}^k$ as

$\vec{y}^k_i = \left\{ \begin{array}{cc} 1 & i = k \\ 0 & \text{otherwise} \end{array} \right\} $

(this is also referred to as the "standard basis vector" $\vec{e}_i$ in $k$-dimensional Euclidean space)

Ex) $\vec{y}^6 = [0, 0, 0, 0, 0, 0, 1, 0, 0, 0]$

Binary cross-entropy loss between an input $\vec{u}$ to the softmax and a 1-hot vector $y_i^{k}$ is defined as

$BCE(\vec{u}, \vec{y^k}) = -\sum_{i} \vec{y}^k_i \log( \sigma_{sm}(\vec{u})_i )$

BCE is 0 if and if only if the outputs of the softmax exactly match the 1-hot vector

Def. Entropy of a probability mass function (PMF) NOTE: A PMF is an array of possible outcomes with the probabilities

Ex) PMF $X = [0:0.2, 1:0.5, 2:0.3]$

$H(X) = \sum_{i} p_i \log_2(1/p_i)$

$H(X) = -\sum_{i} p_i \log_2(p_i)$

Entropy is a measure of the expected number of bits that I should use in an optimal representation of my random variable. Have a look back at Huffman trees from CS 174 for an example of using more bits for less likely things and vice versa.

Cross-entropy is a measure of the expected number of bits that I have to use if I assume the wrong distribution (in this case the output of the softmax) when using probabilities from the target distribution (in this case the 1-hot vector)

import numpy as np
np.log2(1/0.5)

1.0

0.2*np.log2(1/0.2) + 0.5*np.log2(1/0.5) + 0.3*np.log2(1/0.3)

1.4854752972273344

Update Rules

We want the derivatites of the BCE loss with respect to different components $u_i$ of the input $\vec{u}$

$\frac{\partial}{\partial u_i} \left( -\sum_{i} \vec{y}^k_i \log( \sigma_{sm}(\vec{u})_i ) \right)$

There's only one component that actually matters when we're using the one-hot vector $\vec{y}^k_i$

$\frac{\partial}{\partial u_i} \left( - \log( \sigma_{sm}(\vec{u})_k ) \right)$

Case 1:

Let's suppose that $i = k$

By the chain rule, we have

$\frac{\partial}{\partial u_k} \left( - \log( \sigma_{sm}(\vec{u})_k ) \right) = -\frac{1}{\sigma_{sm}(\vec{u})_k } \left( \frac{\partial}{\partial u_k} \sigma_{sm}(\vec{u})_k \right) $

Let's look at the derivative of the inner:

$\frac{\partial}{\partial u_k} \sigma_{sm}(\vec{u})_k = \frac{\partial}{\partial u_k} \frac{e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}} $

Quotient Rule: $f(x) = P(x)/Q(x), f'(x) = (P'(x)Q(x) - Q'(x)P(x))/(Q(x)^2)$

$P(u_k) = e^{u_k}$

$Q(u_k) = \sum_{j = 1}^{L} e^{u_j}$

$P'(u_k) = Q'(u_k) = e^{u_k}$

Therefore,

$\frac{\partial}{\partial u_k} \frac{e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}} = \frac{e^{u_k}(\sum_{j = 1}^{L} e^{u_j}) - e^{u_k} e^{u_k}}{(\sum_{j = 1}^{L} e^{u_j})^2} = \left( \frac{e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}} \right) \left( \frac{(\sum_{j = 1}^{L} e^{u_j}) - e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}} \right) = \sigma_{sm}(\vec{u})_k (1 - \sigma_{sm}(\vec{u})_k) $

Plugging this back into the full derivative of BCE, we get

$ -\frac{1}{\sigma_{sm}(\vec{u})_k } \sigma_{sm}(\vec{u})_k (1 - \sigma_{sm}(\vec{u})_k) $

which simplifies to

$-(1 - \sigma_{sm}(\vec{u})_k)$

For the hot $k$, the update rule is

$u_k \gets u_k + \alpha(1 - \sigma_{sm}(\vec{u})_k)$

In other words, if we're not big enough at our softmax output, we should nudge $u_k$ to the right. This will make $\frac{e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}}$ closer to 1

Case 2:

Let's suppose that $i \neq k$

This is a "cold zero"

$\frac{\partial}{\partial u_i} \left( - \log( \sigma_{sm}(\vec{u})_k ) \right) = - \frac{1}{\sigma_{sm}(\vec{u})_k} \frac{\partial}{\partial u_i} \sigma_{sm}(\vec{u})_k$

Let's take the derivative of the inner using the quotient rule again

$\frac{\partial}{\partial u_i} \sigma_{sm}(\vec{u})_k = \frac{\partial}{\partial u_i} \frac{e^{u_k}}{\sum_{j = 1}^{L} e^{u_j}} $

$P(u_i) = e^{u_k}$

$Q(u_i) = \sum_{j=1}^L e^{u_j}$

Because we're taking the derivative with respect to $u_i$, and $i \neq k$, we treat $u_k$ as a constant. Therefore,

$P'(u_i) = 0$

$Q'(u_i) = e^{u_i}$

and we end up with

$\frac{\partial}{\partial u_i} \sigma_{sm}(\vec{u})_k = \frac{-e^{u_i} e^{u_k}}{(\sum_{j=1}^L e^{u_j})^2} = -\sigma_{sm}(\vec{u})_i \sigma_{sm}(\vec{u})_k $

Plugging this back into the derivative of BCE loss, we have the following incredibly simple expression after a cancellation

$ - \frac{1}{\sigma_{sm}(\vec{u})_k} (-\sigma_{sm}(\vec{u})_i \sigma_{sm}(\vec{u})_k) = \sigma_{sm}(\vec{u})_i$

The update rule for gradient descent for a cold 0 is then

$u_i \gets u_i - \alpha \sigma_{sm}(\vec{u})_i$

In other words, if our softmax output is greater than 0 at our cold 0, we should nudge $u_i$ to the left. This will make $\frac{e^{u_i}}{\sum_{j = 1}^{L} e^{u_j}}$ closer to 0